movmean | MATLAB関数3

MATLAB関数では、MATLABでよく使う関数について便利な使い方とともに紹介しています。前回はsubplotについて紹介しました。今回はmovmeanについて紹介します。

目標の確認

今回作成するfigureを確認しておきます。下の図のように真値(true)に対してノイズを含んだデータ(measured)から移動平均を用いて真値を推測しています(estimated)。

真値データの生成

まずはじめにデータを生成します。真値としてsinカーブのデータを下記で生成しplotで確認します。

t = transpose(0:1:1000);
Data(:,1) = sin(2*pi*t*0.001);
plot(t,Data(:,1));

下の図のようにxが0~1000の1周期のsinカーブが表示されます。

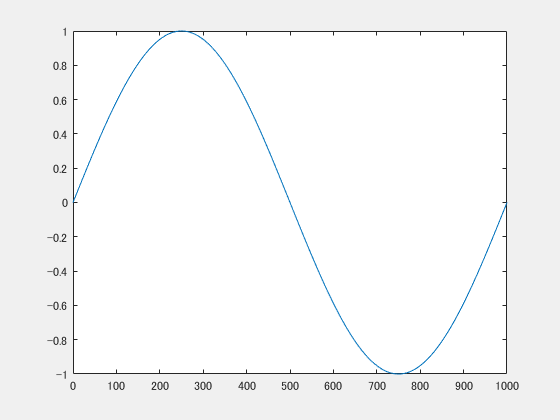
ノイズデータの生成

上記で作成した真値のデータにノイズを下記コードで付与します。

Data(:,2) = Data(:,1) + rand(length(t),1) - 0.5;
plot(t,Data(:,2)

Data(:,1)に対してrandで生成した乱数を足しています。引数のlength(t),1は生成する乱数のサイズを指定しています。

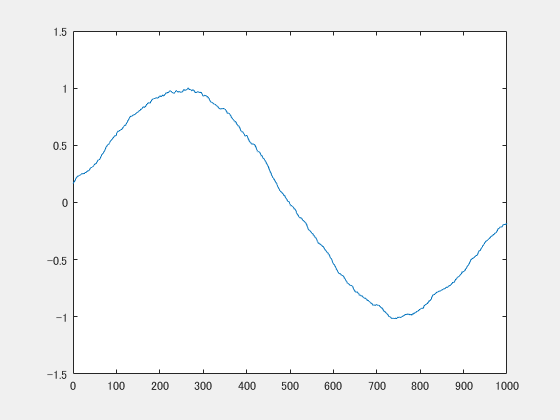
randは区間(0,1)の乱数を生成するため平均値は0.5に近づくはずです。(-0.5,0.5)の乱数とするため、0.5を減算します。　出来上がったグラフは下記のとおりです。

movmeanの使い方

真値は通常知ることができないので、ノイズありのデータから真値を予測したいという場面は多々あります。適切なフィルタを設計して真値を予測することも重要ですが、移動平均を用いて大まかに予想することも必要です。そこでmovmeanを用いれば１行で移動平均の計算が可能です。

Data(:,3) = movmean(Data(:,2),[50 50]);
plot(t,Data(:,3))

「movmean(Data(:,2),[50 50]);」でData(:,2)に対して、現在の点とその前50点、後50点の計101点の平均値を現在の点の値としています。第二引数の[50 50]を[60 40]とすると前60点、後40点と変更することができます。

movmean(Data(:,2),101)のように移動平均に使用する点数を指定することもできます。

真値と比較

それでは真値、ノイズありのデータ、移動平均をまとめて比較します。目標の確認で掲載したグラフが生成されます。

clear;
close all;

t = transpose(0:1:1000);
Data(:,1) = sin(2*pi*t*0.001);
Data(:,2) = Data(:,1) + rand(length(t),1)-0.5;
Data(:,3) = movmean(Data(:,2),[50 50]);

figure(1)
hold on
plot(t,Data(:,1),'r');
plot(t,Data(:,2),'Color','#999999');
plot(t,Data(:,3),'b');
legend('true','measured','estimated');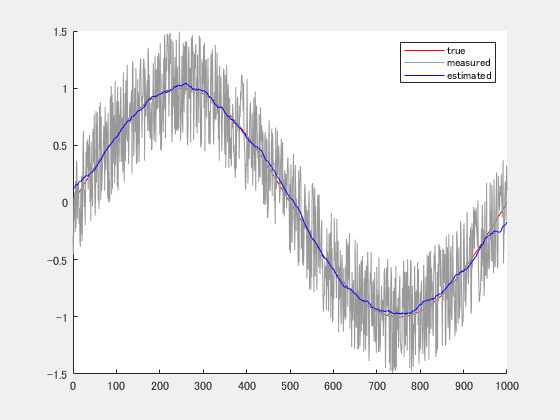

真値が不明な場合には十分役立つ推定値が得られていることがわかります。

余談ですが、ノイズありのデータはグレーにすると見栄えが良くなります。12行目のようにColorを「#999999」に設定すると割と見やすくなります。

movmeanの使い道

移動平均はデータの後処理にはとても便利で、計測データから大まかな傾向を得るときにとても重宝します。

一方で、リアルタイムで計算する場合移動平均は未来の情報も使用していることになります。例えば、株価でよく使用する25日移動平均線などは現在から過去25日間の平均値を求める手法です。MATLABで実装するのであればmovmean(Data,[24 0])となります。現時点での値も含むため第二引数は[24 0]。

これは13日前の時点でのmovmean(Data,[12 12])と同じ値になります。つまり未来のデータが使えない場合、移動平均はかなり実データより遅れた情報になります。

そのため、データの後処理には活用できますが、リアルタイムで処理が必要な場合にはフィルタの設計などが必要になります。

movmeanの注意点

movmeanは移動平均を計算するため、端点に近い箇所では計算に使用する点数が使えない場合があります。その場合使用できる値のみを使って計算します。例えば、movmean(Data,[50 50])の１点目では１点目以前のデータは使用できないため、Data(1:51)の平均値になります。逆に終点の1001番目のデータではData(951:1001)の平均値を使用することになります。

そのため今回のデータの場合始点付近では真値よりも大きめに、終点付近では真値より小さめの値となってしまいます。

まとめ

今回はmovmeanの使い方について説明しました。ノイズありのデータから移動平均を計算するのに非常に便利な関数です。一方で、注意点についても説明しました。リアルタイムで使用する場合やデータの端点付近では注意が必要です。

今回使用したコードは下記に掲載しますので適宜ご活用ください。

clear;
close all;

t = transpose(0:1:1000);
Data(:,1) = sin(2*pi*t*0.001);
Data(:,2) = Data(:,1) + rand(length(t),1)-0.5;
Data(:,3) = movmean(Data(:,2),[50 50]);

figure(1)
hold on
plot(t,Data(:,1),'r');
plot(t,Data(:,2),'Color','#999999');
plot(t,Data(:,3),'b');
legend('true','measured','estimated');